<이 포스팅은 Matlab이 제공하는 Understanding Kalman Filter을 번역 및 요약한 자료입니다. 출처는www.youtube.com/watch?v=VFXf1lIZ3p8 입니다.>
Understanding Kalman Filters, Part 4: Optimal State Estimator Algorithm

- 자율주행 차량의 위치 추정 예제에서, 우리는 single-state(position) 시스템에 대해 위 그림과 같이 모델링하였다.

- 앞의 포스팅에서, 우리는 최적 비편향 추정을 할 수 있는 칼만필터를 통해 차량의 위치를 최소의 분산 값과 함께 추정할 수 있다고 했다.
- 최적 추정은 예측 확률 분포와 측정 확률 분포를 이용해 구할 수 있다.
- 이 두 확률 밀도 함수(pdf)의 곱은 다음과 같은 이산 칼만필터의 식(discrete kalman filter)과 연관된다.

- 이전 포스팅의 상태 관측기(state observer)의 식과 비교해보자.
- 칼만필터는상태 관측기의 한 종류이며, 확률론적 시스템(stochastic system)에 맞추어서 설계되었다.
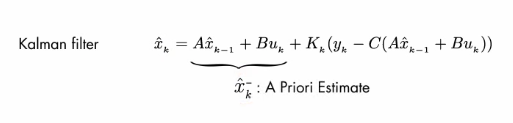
- 이전 상태와 현재 입력을 통해 현재 상태를 구한다.
- 예측 값을 - 을 붙여 표현한다.
- 예측 값은 a priori estimate라고도 불리는데, 이는 현재 측정 값이 들어오기 전에 계산된 값이기 때문이다.

2. 측정 값을 이용해 예측 값(a priori estimate)을 업데이트한다.
- 이를 a posteriori estimate라고 한다.

- 이것이 칼만필터의 알고리즘이다.
- 칼만필터는 Prediction과 Update의 크게 두가지 과정으로 이루어진다.
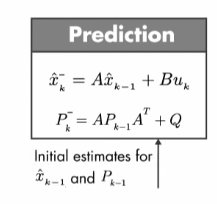
- Prediction에서 시스템 모델은 예측 값(a priori state estimate)과 오차 공분산(error covariance)를 계산한다.
- 단일 상태 시스템(single-state system)에서 P는 예측 값의 분산이다.
- P는 추정 상태의 불확실성을 의미하기도 한다.
- P는 과정 오차(Q)와 이전 스텝에서의 추정 상태 불확실성에서 온다.

- 초기 추정 값과 공분산이 Predition에서 사용된다.
- Prediction에서 계산된 예측 값과 예측 공분산은 추정 값(a posteriori error covariance)와 추정 오차 공분산(a posteriori error covariance)을 구하기 위한 업데이트에 사용된다.
- Kalman gain은 추정 오차 공분산을 최소화한다.
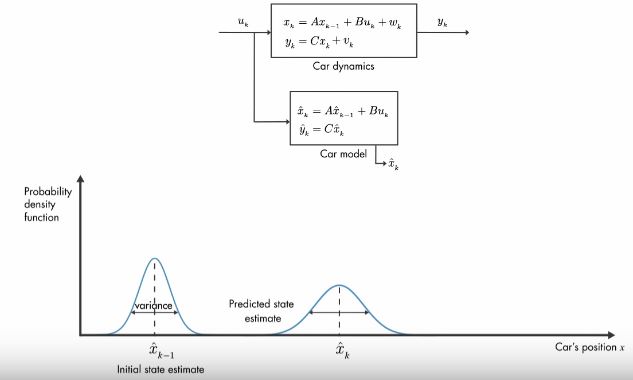
- 칼만 게인은 측정 값과 예측 값이 추정 값에 얼마나 기여하는지를 결정한다.
- 측정 노이즈가 작다면, 측정 값의 신뢰도는 올라가고 추정 값에 기여를 많이 하게된다.
- 예측 값의 오차가 작다면, 마찬가지로 예측 값의 신뢰도가 올라가고, 추정 값에 기여를 많이하게 된다.
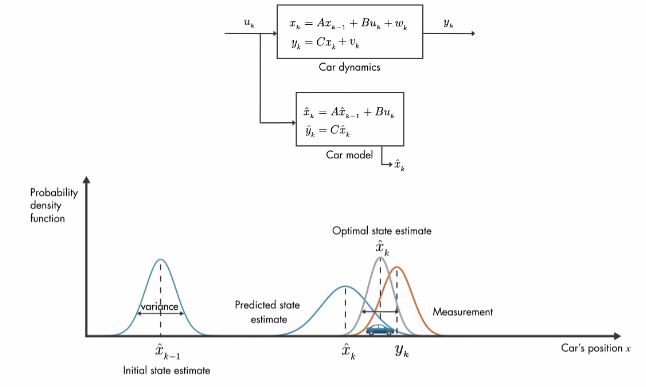
- 이를 수학적으로 표현하면, 첫번째 케이스는 측정 공분산이 0으로 간다고 할 수 있다.
- R(측정 공분산)이 0으로 가면, 칼만 게인은 C의 역행렬이 된다.(현재 시스템에선 1)

- 결국 추정 값은 측정 값으로 수렴한다.
- (위 그림에서 두번째 + -> - 오타)
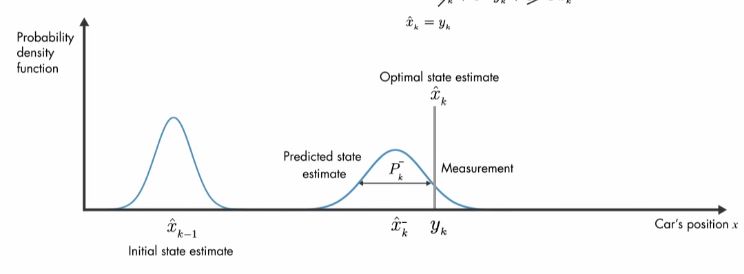
- 측정 공분산이 0일 때를 표현하면 위와 같다.

- 예측 값 오차의 공분산이 0으로 수렴하면, 칼만게인은 0이 된다.
- 따라서 추정 값은 예측 값으로 수렴한다.

- 예측 값 오차의 공분산이 0일 때를 표현하면 위와 같다.

- Update 과정이 완료되면, 추정 값을 이용해 새로운 예측 값을 구한다.
- 이 과정이 반복된다.
- 과정 속에서, 현재 상태를 구할 때, 과거의 정보는 더 이상 필요하지 않다.

- 이전 스텝에서의 추정 상태와 오차 공분산 행렬, 현재 측정 값이 필요할 뿐이다.
- 따라서 칼만필터는 재귀(recursive) 과정이다.

- 만약 측정 값의 상태가 2가지라면 (2가지 센서) 행렬의 차원만 바뀔뿐, 과정은 동일하다.
- plot 상에서는 하나의 pdf가 추가되고, 세 pdf를 사용해 최적 상태 추정을 할 뿐이다.
일반 칼만필터는 선형 시스템에서만 동작한다.
'엔지니어' 카테고리의 다른 글
| [공유] 영상처리 엔지니어 면접 질문 모음 (1) | 2021.08.18 |
|---|---|
| [칼만필터]] 3. 최적 상태 추정기(Optimal State Estimator) (0) | 2020.05.24 |
| [칼만필터] 2. 상태 관측기(State Observer) (2) | 2020.05.24 |
| [칼만필터] 1. 칼만필터란 무엇인가? (0) | 2020.05.24 |



