본 포스팅은 백준 알고리즘 강의 기초2 자료를 바탕으로 작성하였습니다.

그래프
-
정점(Node, Vertex)
-
간선(Edge) : 정점간의 관계
-
G = (V, E)
-
Path

-
Cycle
-
Directed Graph
-
Undirected Graph
-
Multiple Edge
-
Loop : 간선의 양 끝점이 같은 경우

-
Weight
-
Degree : 정점과 연결되어 있는 간선의 개수
- 방향 그래프의 경우 In-degree(들어오는), Out-degree(나가는)로 나누어서 차수를 계산
그래프의 표현
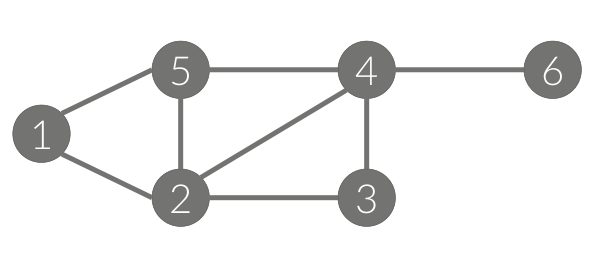
- 정점 : {1,2,3,4,5,6}
- 간선 : {(1,2), (1,5), (2,5), (2,3), (3,4), (2,4), (4,5), (4,6)}

인접 행렬(Adjacency-matrix)
- 이차원 배열 이용
- A[i][j] = 1 (i->j 간선이 있을 때), 0 (없을 때)
- ex) bool a[2000][2000];

인접 리스트(Adjacency-list)
- A[i] = i와 연결된 정점을 리스트로 포함하고 있음
- Linked list나 길이를 동적으로 변경할 수 있는 배열을 사용
- ex) vector<int> g[2000];

- (가중치가 있을 때) A[i] = i와 연결된 정점과 가중치를 리스트로 포함

공간 복잡도
- 인접 행렬 : O(V^2)
- 인접 리스트 : O(E)
간선 리스트(Edge List)
- 배열을 이용해 구한다
- 간선을 모두 저장
- E라는 배열에 간선을 모두 저장
- 각 간선의 앞 정점을 기준으로 개수를 센다
- ex) vector<pair<int,int>> edges;
- ex) edge[i].from, edge[i].to

-
for (int i=0; i<m; i++) { cnt[e[i][0]] += 1; }
for (int i=1; i<=n; i++) {
cnt[i] = cnt[i-1] + cnt[i];
}i번 정점과 연결된 간선은 E배열에서 cnt[i-1]부터 cnt[i]-1까지이다
깊이 우선 탐색(DFS)
- 스택을 이용해 갈 수 있는 만큼 최대한 많이 가고
- 갈 수 없으면 이전 정점으로 돌아감

void dfs(int x) {
check[x] = true;
for (int i=1; i<=n; i++) {
if (a[x][i] == 1 && check[i] == false) {
dfs(i);
}
}
}인접 행렬을 이용한 구현
void dfs(int x) {
check[x] = true;
for (int i=0; i<a[x].size(); i++) {
int y = a[x][i];
if (check[y] == false) {
dfs(y);
}
}
}인접 리스트를 이용한 구현
너비 우선 탐색(BFS)
- 큐를 이용해서 지금 위치에서 갈 수 있는 것을 모두 큐에 넣는 방식
- 큐에 넣을 때 방문했다고 체크

-
queue<int> q; check[1] = true; q.push(1); while (!q.empty()) { int x = q.front(); q.pop(); for (int i=1; i<=n; i++) { if (a[x][i] == 1 && check[i] == false) { check[i] = true; q.push(i); } } } -
인접 행렬 방식
queue<int> q;
check[1] = true; q.push(1);
while (!q.empty()) {
int x = q.front(); q.pop();
for (int i=0; i<a[x].size(); i++) {
int y = a[x][i];
if (check[y] == false) {
check[y] = true; q.push(y);
}
}
}인접 리스트 방식
시간 복잡도
- 인접 행렬: O(V^2 )
- 인접 리스트: O(V+E)
'프로그래머 > 알고리즘' 카테고리의 다른 글
| [해커랭크 C++] Exceptional Server (0) | 2021.01.21 |
|---|---|
| [BOJ] 1707번 - 이분 그래프 (0) | 2020.06.05 |
| [BOJ] 11724번 - 연결요소의 개수 (0) | 2020.06.05 |
